Linear List
注意:下面算法描述是采用go语言编写 完整示例代码
线性表
线性表是一种具有 \(n\) 个相同元素 \((n >= 0)\) 的有限序列
$$L = \{a_{1},\ a_{2},\ a_{3}, \ ...,\ a_{n}\}$$
它们须满足:
存在逻辑上的第一个元素
中间元素具有唯一的前驱和后继
存在逻辑上的最后一个元素
注:循环链表也是一种线性表(尽管在存储上是非线性结构)
综上所述,线性表只是一种逻辑结构
顺序表
顺序表是一种线性表的存储结构,其具有随机访问的特点,但是插入,删除需要移动大量元素,因为元素不需要存储额外信息,所以顺序表的存储密度比较高. 顺序表一般用数组和一个长度指示器表示,比如写成go的结构体如下://constant for seqlist max length
const maxSIZE = 1 << 16
type seqList struct {
length int64
data [maxSIZE]interface{}
}
导入库
import (
"errors"
"reflect"
"sort"
// "fmt"
)
错误处理
var (
OutOfRangeIndex = errors.New("OutOfRangeIndex")
TypeError = errors.New("TypeError")
UnExpectedType = errors.New("UnExpectedType")
OperationWithEmpty = errors.New("OperationWithEmpty")
NotSupportCompare = errors.New("NotSupportCompare")
IsNotSorted = errors.New("IsNotSorted")
)
模拟泛型
实现算法前出现了大问题,go的泛型支持比较弱,interface{}之间的比较需要通过类型断言或反射来完成,所以为了弥补其缺陷,我们编写compare函数来模拟传统的 \(>,<,=\) 等操作符,compare实现并不复杂,只是需要大量的类型断言(写的有点手累,我们可以先实现一些用来调试的类型,把更多的精力关注算法本身),此外通过定义常量来表示比较结果,以及前述的NotSupportCompare来表示一些不可比较的类型作compare参数的错误const (
LessThan = -1
Eq = 0
GreaterThan = 1
UnCompareable = 2
)
func compare(left interface{},right interface{}) (status int, err error) {
if reflect.TypeOf(left).Kind() != reflect.TypeOf(right).Kind() {
return UnCompareable,UnExpectedType
}
//ps:switch 的局限性导致大量重复代码
switch right := right.(type) {
case int:
left := left.(int)
if left < right {
return LessThan,err
} else if left > right {
return GreaterThan,err
} else {
return Eq,err
}
case string:
left := left.(string)
if left < right {
return LessThan,err
} else if left > right {
return GreaterThan,err
} else {
return Eq,err
}
case float32:
left := left.(float32)
if left < right {
return LessThan,err
} else if left > right {
return GreaterThan,err
} else {
return Eq,err
}
//ignore int32,int64,uint32,float64 throw to default
default:
return UnCompareable,NotSupportCompare
}
}
有序顺序表
为了提供向有序表的转化,我们先实现sort包里sort.Interface的接口,然后我们就可以通过sort包里提供的函数进行排序(当然排序算法以后也会提到,暂时先使用标准库的),为了实现sort.Interface,我们需要完成一下函数的编写/*
为seqlist实现sort.Interface接口
*/
func (seq SeqList) Len() int {
return int(seq.Length())
}
func (seq SeqList) Less(i int,j int) bool {
status,err := compare(seq.data[i],seq.data[j])
if err != nil {
panic("not Compareable")
}
if status == LessThan {
return true
}
return false
}
func (seq SeqList) Swap(i, j int) {
temp := seq.data[i]
seq.data[i] = seq.data[j]
seq.data[j] = temp
}
// notice: no check for the type
func (seq SeqList) ConvertToSorted() {
sort.Sort(seq)
}
顺序表的创建
为了获得顺序表,我们需要构造的方法,这里定义了两种,此外不使用原生的seqList,而是使用其指针(type SeqList = *seqList),主要是因为go的方法接收者是结构体时会创建其结构的副本进行调用方法,而对原对象不产生影响,故我们使用其指针,并导出.type SeqList = *seqList
// create SeqList
func New(element interface{},length int64) (seq SeqList,err error) {
var seqlist seqList
if length > maxSIZE || length < 0 {
return nil,OutOfRangeIndex
}
seqlist.length = length
for i := int64(0); i < length; i++ {
seqlist.data[i] = element
}
return &seqlist,err
}
func NewWith(elements interface{}) (seq SeqList,err error) {
var seqlist seqList
seqlist.length = 0
rawValue := reflect.ValueOf(elements)
switch rawValue.Kind() {
case reflect.Slice,reflect.Array:
err = seqlist.checkAdding(int64(rawValue.Len()))
if err != nil {
return nil,err
}
for i := 0; i < rawValue.Len(); i++ {
seqlist.data[i] = rawValue.Index(i).Interface()
}
seqlist.length = int64(rawValue.Len())
return &seqlist,err
default:
return nil,UnExpectedType
}
}
// return the length of seqList
func (seq SeqList) Length() int64 {
return seq.length
}
// judge whether is empty seqlist
func (seq SeqList) IsEmpty() bool {
return seq.length == 0
}
//check the operation's index
func (seq SeqList) checkIndex(index int64) (err error) {
if index < 0 || index >= seq.length {
return OutOfRangeIndex
}
return err
}
// check the rest cap of seqlist
func (seq SeqList) checkAdding(cap int64) (err error) {
if cap < 0 || (seq.length + cap) >= maxSIZE {
return OutOfRangeIndex
}
return err
}
// check the type whether is identical
func (seq SeqList) checkType(element interface{}) (err error) {
if seq.IsEmpty() {
return err
}
expectedType := reflect.TypeOf(seq.data[0]).Kind()
rawType := reflect.TypeOf(element).Kind()
if expectedType != rawType {
err = TypeError
}
return err
}
/*
时间复杂度:O(1)
空间复杂度:O(1)
*/
func (seq SeqList) Get(index int64) (value interface{},err error) {
err = seq.checkIndex(index)
if err != nil {
return nil,err
}
return seq.data[index],err
}
/*
时间复杂度: O(1)
空间复杂度: O(1)
*/
func (seq SeqList) Modify(index int64,element interface{}) (err error) {
err = seq.checkIndex(index)
if err != nil {
return err
}
err = seq.checkType(element)
if err != nil {
return err
}
seq.data[index] = element
return err
}
顺序表的索引规律
我们一般用数组来表示顺序表存储数据,大多数编程语言(lua例外)以 \(0 \ ... \ length - 1\) 来表示序列的索引,为了讨论更广泛(包含子序列),我们设序列
$$S = a_{low}a_{low+1} \cdots a_{high}
\quad (low \leq high)$$
序列长度 \(Length\)
由数学规律可知
$$Length = high - low + 1$$
序列的索引
中点索引
中点索引很明显与序列长度,是奇还是偶有关,比如说序列 \(\{0,1,2,3,4,\}\) 长度为5,我们也很容易观察到其中点索引为2,中点元素也为2,而对于序列 \(\{0,1,2,3\}\) ,我们很难说明其中点索引,所以我们规定其有两个中点索引,分为左中点索引,右中点索引,分别记为符号 \(leftmiddle,rightmiddle\) ,而上述序列左中点索引就为1,其元素为1,右中点索引为2,其元素为2,至此我们可以推出其中点索引 \(middleIndex\) 的表达式
注意:下述计算结果都是整型,在强类型语言中一般都经过向下取整操作,动态语言中比如js,要显式调用floor向下取整函数
$$
middleIndex = \begin{cases}
(high + low) \ / \ 2 \\
(high + low + 1) \ / \ 2
\end{cases} \quad (Length为奇数)
$$
在Length是奇数的情况下,
\((high + low) \ / \ 2 \)
和
\((high + low + 1) \ / \ 2\)
是相等的
$$
middleIndex = \begin{cases}
leftmiddle = (high + low) \ / \ 2 \\
rightmiddle = (high + low + 1) \ / \ 2
\end{cases} (Length是偶数)
$$
其实
\(rightmiddle = leftmiddle + 1 = (high + low) \ / \ 2 + 1\)
,在向下取整和
\(Length\)
是偶数的作用下上述等式都是成立的
思维转换:先考虑
\(a_{0}a_{1} \cdots a_{high}\)
,其长度为
\(high + 1\)
,故其中点索引为
\(middleIndex = (high + 1) / 2\)
(可以考虑下high为奇数还是偶数,若high为偶数等式还可以写成
\(middleIndex = (high) / 2 \quad high为偶数\)
),若序列为
\(a_{low}a_{low+1} \cdots a_{high}\)
,只需要将
\(middleIndex\)
平移
\(low\)
就能得到上述等式
......
顺序表的插入操作
顺序表的插入需要移动指定索引后的大量元素,实现也特别简单,时间复杂度为 \(O(n)\) ,空间复杂度为 \(O(1)\) ,下面为其实现:/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) InsertByIndex(index int64,element interface{}) (err error) {
err = seq.checkType(element)
if err != nil {
return err
}
err = seq.checkIndex(index)
if err != nil {
return err
}
err = seq.checkAdding(1)
if err != nil {
return err
}
for i := seq.length; i != index; i-- {
seq.data[i] = seq.data[i - 1]
}
seq.data[index] = element
return err
}
顺序表的删除
顺序表按索引删除操作特别简单,需要将指定索引后元素向前移动一格,时间复杂度为 \(O(n)\) ,空间复杂度为 \(O(1)\)/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) DeleteByIndex(index int64) (err error) {
err = seq.checkIndex(index)
if err != nil {
return err
}
for i := index; i < seq.length - 1; i++ {
seq.data[i] = seq.data[i + 1]
}
seq.length = seq.length - 1
return err
}
/*
时间复杂度: O(n)
空间复杂度: O(1)
fixme: now the operator "<" is supported with
number,string type
*/
func (seq SeqList) DeleteMin() (err error) {
if seq.length <= 0 {
return OperationWithEmpty
}
minIndex := int64(0)
for i := int64(1); i < seq.length; i++ {
status,err := compare(seq.data[i],seq.data[minIndex])
if err != nil {
return err
}
if status == LessThan {
minIndex = i
}
}
// O(n)操作
return seq.DeleteByIndex(minIndex)
}
注意:下面给出了在seq_test.go文件里对编写的算法的测试,
后面的算法将不放出测试用例,你可以自行编写函数进行测试,使其覆盖率更高
//seq_test.go
package sequence
import "testing"
import (
// "fmt"
)
func checkError(err error,t *testing.T) {
switch err {
case nil:
return
case OutOfRangeIndex:
t.Error("OutOfRangeIndex")
case TypeError:
t.Error("TypeError")
case UnExpectedType:
t.Error("UnExpectedType")
case OperationWithEmpty:
t.Error("OpeationWithEmpty")
case NotSupportCompare:
t.Error("NotSupportCompare")
case IsNotSorted:
t.Error("IsNotSorted")
default:
t.Error("should unreached")
return
}
}
func TestDeleteByIndex(t *testing.T) {
seq,err := NewWith([]int{1,2,3,4,5})
checkError(err,t)
err = seq.DeleteByIndex(2)
checkError(err,t)
if seq.data[2] != 4 {
t.Error("func DeleteByIndex's result unexpected")
}
}
func TestDeleteMin(t *testing.T) {
seq,err := NewWith([]int{6,1,3,4,5})
checkError(err,t)
err = seq.DeleteMin()
checkError(err,t)
if seq.data[1] != 3 {
t.Error("func DeleteMin's result unexpected")
}
}
/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) deleteAllWithIdenticalTag(elem interface{}) (err error) {
if seq.IsEmpty() {
return OperationWithEmpty
}
//set identical element's count
var k int64 = 0
for i := int64(0); i < seq.length; i++ {
status,err := compare(seq.data[i],elem)
if err != nil {
return err
}
if status != Eq {
seq.data[i - k] = seq.data[i]
} else {
k++
}
}
//update seqlist's length
seq.length = seq.length - k
return err
}
func (seq SeqList) deleteAllWithDifferentTag(elem interface{}) (err error) {
if seq.IsEmpty() {
return OperationWithEmpty
}
// set different element's count
var k int64 = 0
for i := int64(0); i < seq.length; i++ {
status,err := compare(seq.data[i],elem)
if err != nil {
return err
}
if status != Eq {
seq.data[k] = seq.data[i]
k++
}
}
seq.length = k
return err
}
func (seq SeqList) DeleteAll(elem interface{}) (err error) {
//return seq.deleteAllWithIdenticalTag(elem)
return seq.deleteAllWithDifferentTag(elem)
}
/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) DeleteRangeElem(start interface{},end interface{}) (err error) {
if seq.IsEmpty() {
return OperationWithEmpty
}
status,err := compare(start,end)
if err != nil {
return err
}
if status == GreaterThan {
return OperationWithEmpty
}
//counter for elements of between start and end
var k int64 = 0
for i := int64(0); i < seq.length; i++ {
left,err := compare(seq.data[i],start)
if err != nil {
return err
}
right,err := compare(seq.data[i],end)
if err != nil {
return err
}
if left == LessThan || right == GreaterThan {
seq.data[i - k] = seq.data[i]
} else {
k++
}
}
if k == 0 {
err = OperationWithEmpty
}
//update the seqlist's length
seq.length = seq.length - k
return err
}
/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) DeleteRangeElemWithSorted(start interface{},end interface{}) (err error) {
if seq.IsEmpty() {
return OperationWithEmpty
}
status,err := compare(start,end)
if err != nil {
return err
}
if status == GreaterThan {
return OperationWithEmpty
}
if !sort.IsSorted(seq) {
return IsNotSorted
}
err = seq.checkType(start)
if err != nil {
return err
}
//start index,end index
var sindex int64
var eindex int64
for sindex = 0; sindex < seq.length; sindex++ {
status,err = compare(seq.data[sindex],start)
if err != nil {
return err
}
if status != LessThan {
break
}
}
for eindex = sindex; eindex < seq.length; eindex++ {
status,err = compare(seq.data[eindex],end)
if err != nil {
return err
}
if status == GreaterThan {
break
}
}
//compute the total count of that should delete
//notice seq.data[eindex] > end,so ....
total := eindex - sindex
if total <= 0 {
return OperationWithEmpty
}
//begin delete
for i := eindex; i < seq.length; i++ {
seq.data[i - total] = seq.data[i]
}
//update seqlist length
seq.length = seq.length - total
return err
}
注意:也可把有序顺序表当成无序顺序表来删除,两者时间复杂度都是
\(O(n)\)
,并没有体现有序顺序表的优越性
我们接着考虑有序顺序表删除重复元素的操作(只留下重复元素的一个),因为顺序表是有序的,重复元素区间必定是连续的,我们只需要在遍历过程中记录非重复元素位置,接着在遇到下一个非重复元素时将其移动到上一个非重复元素位置的后继即可,待到遍历结束,修改顺序表的length便完成了删除的操作,因此其时间复杂度为
\(O(n)\)
,空间复杂度为
\(O(1)\)
/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) DeleteRepeatElemWithSorted() (err error) {
if seq.IsEmpty() {
return OperationWithEmpty
}
if !sort.IsSorted(seq) {
return IsNotSorted
}
//the begining of not unrepeat element
var k int64 = 0
for i := int64(1); i < seq.length; i++ {
status,err := compare(seq.data[i],seq.data[k])
if err != nil {
return err
}
if status != Eq {
k++
seq.data[k] = seq.data[i]
}
}
seq.length = k + 1
return err
}
顺序表的逆序操作
对于顺序表的逆序操作,为了使考虑不失一般性,我们先来考虑对于子序列 \(S[low...high]\) 的逆序操作,对于长度为奇数的序列,我们只要将序列中除中点索引外的所有索引元素首尾交换即可,而对于长度为偶数的序列,所有的元素都会被首尾交换,左中点和右中点索引元素交换,综上我们可以得出,以上算法就是完成序列索引 \([low,leftmiddle]\) 与 \([rightmiddle,high]\) 元素的首尾互换(对于长度为偶数的序列左中点与右中点索引相同),因此时间复杂度为 \(O(n)\) ,空间复杂度为 \(O(1)\)/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) ReverseWithRange(start int64,end int64) (err error) {
if seq.checkIndex(start) != nil || seq.checkIndex(end) != nil {
return OutOfRangeIndex
}
if start >= end {
return OperationWithEmpty
}
var k int64 = (end + start + 1) / 2
for i := int64(start); i < k; i++ {
temp := seq.data[i]
seq.data[i] = seq.data[end + start - i]
seq.data[end + start - i] = temp
}
return err
}
/*
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) Reverse() (err error) {
return seq.ReverseWithRange(0,seq.length - 1)
}
逆序操作的应用
我们可以通过逆序操作来实现序列一些有规律的重排列,比如考虑将序列 \(a_{1}a_{2} \cdots a_{s}b_{1}b_{2} \cdots b_{t}\) 重排列为 \(b_{1}b_{2} \cdots b_{t}a_{1}a_{2} \cdots a_{s}\) ,这里我只需要3次逆序便可完成,第一次整个序列逆序为 \(b_{t}b_{t - 1} \cdots b_{2}b_{1}a_{s}a_{s - 1} \cdots a_{2}a_{1}\) ,第二次将子序列 \(b_{t}b_{t - 1} \cdots b_{2}b_{1}\) 逆序为 \(b_{1}b_{2} \cdots b_{t}\) 第三次将子序列 \(a_{s}a_{s-1} \cdots a_{2}a_{1}\) 逆序为 \(a_{1}a_{2} \cdots a_{s}\) 这样就完成了实现,三次逆序都是 \(O(n)\) 操作,故其时间复杂度为 \(O(n)\) ,空间复杂度为 \(O(1)\)/*
example the seqlist is: b1b2b3....bma1a2....an
index = m
after the operation the seqlist is a1a2...anb1...bm
时间复杂度: O(n)
空间复杂度: O(1)
*/
func (seq SeqList) LocalSwapFrom(index int64) (err error) {
err = seq.checkIndex(index)
if err != nil {
return err
}
err = seq.ReverseWithRange(0,seq.length - 1)
if err != nil {
return err
}
err = seq.ReverseWithRange(0,seq.length - (index + 1) - 1)
if err != nil {
//ignore the operation with empty
if err != OperationWithEmpty {
return err
}
}
err = seq.ReverseWithRange(seq.length - (index + 1),seq.length - 1)
if err != nil {
//ignore the operation with empty
if err != OperationWithEmpty {
return err
}
}
err = nil
return err
}
/*
example: we have a0a1a2....apap+1....as
n = p
the result is apap+1...asa0a1....ap-1
*/
func (seq SeqList) CycleMoveLeftN(n int64) (err error) {
if n < 0 || n > seq.length {
return OutOfRangeIndex
}
if n == 0 || n == seq.length {
return OperationWithEmpty
}
err = seq.ReverseWithRange(0,seq.length - 1)
if err != nil {
return err
}
err = seq.ReverseWithRange(0,seq.length - n - 1)
if err != nil {
//ignore empty empty operation
if err != OperationWithEmpty {
return err
}
}
err = seq.ReverseWithRange(seq.length - n,seq.length - 1)
if err != nil {
//ignore empty operation
if err != OperationWithEmpty {
return err
}
}
return err
}
顺序表的查找
对于无序顺序表的查找,一般就是直接暴力查找了,但是对于有序顺序表的查找,我们可以采用二分查找,减少时间复杂度,其时间复杂度为 \(O(\log n)\) ,空间复杂度为 \(O(1)\) ,当然也可以用递归来写/*
时间复杂度: O(logn)
空间复杂度: O(1)
*/
func (seq SeqList) BinarySearchWithSorted(elem interface{}) (index int64,err error) {
if seq.IsEmpty() {
return -1,OperationWithEmpty
}
if !sort.IsSorted(seq) {
return -1,IsNotSorted
}
var low int64 = 0
var high int64 = seq.length - 1
var middle int64
for ; low <= high; {
middle = (high + low) / 2
status,err := compare(elem,seq.data[middle])
if err != nil {
return -1,err
}
if status == Eq {
return middle,err
} else if status == LessThan {
high = middle - 1
} else {
low = middle + 1
}
}
return -1,OperationWithEmpty
}
$$S.length = 2 * A.length = 2 * B.length$$
故无论
\(A\)
和
\(B\)
的长度是奇数还是偶数,S的长度都是偶数,而且我们很容易得知对于S,剔除在首尾共计
\(A.length\)
个元素后得到的子序列
\(S^{'}\)
中依然存在着原序列
\(S\)
的中位数,我们不断迭代或递归剔除算法,必定得到剩余两个元素的子序列
\(S^{*}\)
(证明过其长度必定为偶数),此时
\(S^{*}[0]\)
便为原序列
\(S\)
的中位数
下面介绍如何找到其剔除的元素,我们先来讨论
\(A.length为偶数的情况\)
,此时可知我们需要在左右分别剔除
\(A.length / 2\)
个元素,接着我们假设
\(a_{middle} > b_{middle}\)
(
\(a_{middle} < b_{middle}\)
的情况与之类似,
\(a_{middle} = b_{middle}\)
的情况后面讨论)
,由于
\(a_{middle} > b_{middle}\)
,故我们可以得到
对于
\(
\forall a_{k} \in \{a_{middle+1},a_{middle+2},\cdots , a_{n-1}\} \quad
\forall a_{i} \in \{a_{0},a_{1}, \cdots , a_{middle}\} \quad
\forall b_{j} \in \{b_{0},b_{1},b_{3}, \cdots ,b_{middle}\}
\)
,都有
\(a_{k} \gt a_{i}\)
且
\(a_{k} \gt b_{j}\)
,故可得到子序列
\(M = a_{middle+1}a_{middle+2} \cdots a_{n - 1}\)
中任意元素大于序列
\(N = a_{0}a_{1} \cdots a_{middle}b_{0}b_{1} \cdots b_{middle}\)
中任意元素,设序列
\(N\)
的升序序列为
\(N^{'}\)
,故
$$N.length = N^{'}.length = 2 * middle = n$$
,故序列
\(M\)
在序列
\(S\)
中左边至少有
\(A.length\)
个元素,因此序列
\(M\)
中不包含中位数,故可在序列
\(S\)
中剔除序列
\(M\)
中的元素,同样我们可以尝试剔除序列
\(S\)
左边的部分,下面我们来证明和寻找左边的部分,通过之前的式子,我们还可以知道
对于
\(\forall b_{k} \in \{b_{0},b_{1},b_{2}, \cdots b_{middle}\} \quad \forall b_{i} \in \{b_{middle+1},b_{middle+2},\cdots b_{n-1}\} \quad \forall a_{j} \in \{a_{middle},a_{middle+2},\cdots, a_{n-1}\}\)
,都有
\(b_{k} \lt b_{i}\)
且
\(b_{k} \lt a_{j}\)
,故可得到对于子序列
\(P = b_{0}b_{1} \cdots b_{middle}\)
中任意元素都小于
序列
\(Q = b_{middle+1}b_{middle+2} \cdots b_{n-1}a_{middle}a_{middle+1} \cdots a_{n-1}\)
,设序列
\(Q\)
的升序序列为
\(Q^{'}\)
,故
$$Q.length = Q^{'}.length = 2 * middle + 1 = n + 1$$
,因此子序列
\(P\)
在序列
\(S\)
中小于右边至少
\(n+1\)
个元素,而
\(S\)
的中位数是第
\(n\)
位元素,小于右边
\(n\)
个元素,因此序列
\(P\)
不包含
\(S\)
的中位数,从而可以从
\(S\)
中剔除
\(P\)
,因此我们从序列
\(A\)
中剔除
\(M\)
得到
\(A{'}\)
,从
\(B\)
中剔除
\(P\)
得到
\(B^{'}\)
,
而
\(A^{'}\)
和
\(B^{'}\)
都是升序序列,且
$$A^{'}.length = B^{'}.length = middle$$
,满足循环不变式且算法规模减小,故最后能够得到结果
下面我们来讨论一下, \(A和B长度都是奇数的情况下\) ,这里还是假设 \(a_{middle} > b_{middle}\) ,故 对于 \(\forall a_{k} \in \{a_{middle}a_{middle+1} \cdots a_{n-1}\} \quad \forall a_{i} \in \{a_{0}a_{1} \cdots a_{middle-1}\} \quad \forall b_{j} \in \{b_{0}b_{1} \cdots b_{middle}\} \) 都有 \(a_{k} \gt a_{i}\) 且 \(a_{k} \gt b_{j}\) ,故可得到子序列 \(J = a_{middle}a_{middle+1} \cdots a_{n-1}\) 中任意元素都大于 序列 \(R = a_{0}a_{1} \cdots a_{middle-1}b_{0}b_{1}b_{middle}\) 中的元素,设序列 \(R\) 的升序序列为 \(R^{'}\) ,则
$$R^{'}.length = R.length = n$$
,故子序列
\(J\)
在序列
\(S\)
中的左边至少存在
\(n\)
个元素,而
\(S\)
的中位数是第n个元素,故子序列
\(J\)
中不存在
\(S\)
的中位数,故可在序列
\(S\)
中剔除
\(J\)
,此外我们还有,对于
\(\forall b_{k} \in \{b_{0},b_{1}, \cdots, b_{middle-1}\} \quad
\forall b_{i} \in \{b_{middle},b_{middle+1}, \cdots, b_{n-1}\} \quad
\forall a_{j} \in \{a_{middle},a_{middle+1}, \cdots , a_{n-1}\}
\)
都有
\(b_{k} < b_{i}\)
且
\(b_{k} < a_{j}\)
,即对于子序列
\(T = b_{0}b_{1} \cdots b_{middle-1}\)
中任意元素都小于
\(Y = a_{0}a_{1} \cdots a_{middle}b_{0}b_{1} \cdots b_{middle}\)
中任意元素,设序列
\(Y\)
升序序列为
\(Y^{'}\)
,故
$$Y^{'}.length = Y.length = n + 1$$
因此子序列
\(T\)
在序列
\(S\)
中的右边至少小于
\(n+1\)
个元素,而中位数在小于
\(n\)
个元素的位置,故
\(T\)
中不存在中位数元素,可在
\(S\)
中剔除
\(T\)
,因此我们从序列
\(A\)
中剔除
\(J\)
得到
\(A^{'}\)
\(B\)
中剔除
\(T\)
得到
\(B^{'}\)
,我们有
\(A^{'},B^{'}\)
都为升序序列且
\(A^{'}.length = B^{'}.length = middle + 1\)
,故以
\(A^{'},B^{'}\)
保持循环不变式成立且算法规模减小,故可求得解
通过以上步骤我们也可证得当
\(a_{middle} = b_{middle}\)
的情况,无论
\(A.length是否为奇数和偶数\)
我们都有,对于
\(\forall a_{i} \in H = \{a_{0},a_{1}, \cdots , a_{middle-1}\} \quad
\forall b_{k} \in K = \{b_{0},b_{1}, \cdots , b_{middle-1}\}
\)
,我们都有
\(a_{middle} \ge a_{i}\)
且
\(a_{middle} \ge b_{k}\)
而
\(H.length + K.length = 2 * middle = n\)
,故可知位于序列
\(S\)
第
\(n\)
位的中位数必定等于
\(a_{middle}\)
,故可得出此时序列
\(S\)
的中位数等于
\(a_{middle}\)
,结束算法
通过算法实现我们知道其时间复杂度为
\(O(\log{n})\)
,空间复杂度为
\(O(1)\)
/*
left: a1a2....an
right: b1b2b3...bn
*/
func FindMiddleWithTwoSortedEqualLengthSequence(left SeqList,right SeqList) (elem interface{},err error) {
if left.length != right.length {
return nil,OutOfRangeIndex
}
if left.IsEmpty() {
return nil,OperationWithEmpty
}
if !sort.IsSorted(left) || !sort.IsSorted(right) {
return nil,IsNotSorted
}
// find the middle of left
var leftLow,rightLow = int64(0),int64(0)
var leftHigh,rightHigh = left.length - 1,right.length - 1
for ; leftLow < leftHigh && rightLow < rightHigh; {
leftMiddle := (leftHigh + leftLow) / 2
rightMiddle := (rightHigh + rightLow) / 2
leftMiddleElem := left.data[leftMiddle]
rightMiddleElem := right.data[rightMiddle]
status,err := compare(leftMiddleElem,rightMiddleElem)
if err != nil {
return nil,err
}
if status == Eq {
return leftMiddleElem,err
} else if status == LessThan {
// 元素为奇数
if (leftLow + leftHigh) % 2 == 0 {
leftLow = leftMiddle
rightHigh = rightMiddle
} else {
leftLow = leftMiddle + 1
rightHigh = rightMiddle
}
} else {
if (rightLow + rightHigh) % 2 == 0 {
rightLow = rightMiddle
leftHigh = leftMiddle
} else {
rightLow = rightMiddle + 1
leftHigh = leftMiddle
}
}
}
leftMiddleElem := left.data[leftLow]
rightMiddleElem := right.data[rightLow]
status,err := compare(leftMiddleElem,rightMiddleElem)
if err != nil {
return nil,err
}
if status == LessThan {
return leftMiddleElem,err
} else {
return rightMiddleElem,err
}
}
func (seq SeqList) FindMajorElement() (elem interface{},err error) {
if seq.IsEmpty() {
return nil,OperationWithEmpty
}
//the major element occur count
var count int64 = 1
majorElement := seq.data[0]
for i := int64(1); i < seq.length; i++ {
status,err := compare(majorElement,seq.data[i])
if err != nil {
return nil,err
}
if status == Eq {
count++
} else {
if count > 0 {
count--
} else {
majorElement = seq.data[i]
count = 1
}
}
}
if count > 0 {
count = 0
for i := int64(0); i < seq.length; i++ {
status,err := compare(seq.data[i],majorElement)
if err != nil {
return nil,err
}
if status == Eq {
count++
}
}
if count > seq.length / 2 {
return majorElement,err
}
} else {
return nil,OperationWithEmpty
}
return nil,OperationWithEmpty
}
链表
链表是一种线性表的存储结构,它不严格使用连续的内存,而是通过保存前驱或后继的地址,保持线性表的逻辑结构.它与顺序表主要的区别是它随机访问慢,因为保存了与数据信息无关的前驱或后继地址,所以存储密度较低,但是插入和删除具有较好的性能. 链表也有不同的种类,主要有单链表(只带后继指针,尾指针后继指针为空),循环单链表(只带后继指针,但尾指针后继指针指向头指针),双链表(结点指针带前驱和后继指针,头指针前驱和尾指针后继都为空),循环双链表(结点指针带前驱和后继指针,头指针前驱为尾指针,尾指针后继为头指针)等 链表还被分为带头结点和不带头结点的方式处理
注:结点和结点指针是不同的,结点代表的是存储对象实体,而结点指针代表的是指向存储对象地址(没有指向时为空)
因此带头结点处理就是创建空链表时浪费结点数据的大小存储空间,使头指针指向创建好的头结点(该结点不存储应用数据),而这样的目的就是编写链表处理函数时方便处理,统一逻辑(因为真正开始存储数据的结点也有前驱,和其它结点并无区别)
而不带头结点的链表指的是创建链表时,头指针指向空,因为此时真正开始存储数据的结点就是头指针指向的,但它没有前驱了,因此编写处理函数需要特殊对待,但它也具有节省存储空间的优点.
下面介绍一下代码使用的结构体(其他辅助操作,前面和源代码都有,不再赘述),因为算法比较多,这里也只介绍一下常见的算法和主要的思路.(这里使用的是不带头结点的单链表)
type Node = *node
type node struct {
data interface{}
next Node
}
/*
we use no head node linklist
*/
type LinkList = *linkList
type linkList struct {
head Node
}
链表的插入
链表的插入分为头插入和尾插入法,顾名思义,头插入法是将头指针指向插入的新节点,并且新节点的后继是以前头指针指向的结点,所以对于头插入法,我们首先要更改插入结点的后继,然后更改头指针,使其指向插入结点,来看下描述代码func (list LinkList) PushFront(elem Node) {
elem.next = list.head
list.head = elem
}
func (list LinkList) PushBack(elem Node) {
elem.next = nil
if list.head == nil {
list.head = elem
} else {
for current := list.head; current.next != nil; current = current.next {
}
current.next = elem
}
}
链表的删除
链表的删除需要注意的是单链表在遍历过程中需要保存删除结点的前驱指针,如果采用的是不带头结点的单链表,则其前驱为空需要被分为特殊情况,删除时若前驱指针为空,则表示此时删除的是头指针指向的结点,所以只需修改头指针即可,如果删除的结点前驱指针不为空,则表示删除的不是头指针指向的结点,此时需要更改前驱指针指向删除结点的后继(非gc语言要记得释放删除结点内存),下面是描述代码func (list LinkList) DeleteAll(elem interface{}) (err error) {
if list.IsEmpty() {
return OperationWithEmpty
}
var pre Node = nil
deleted := false
for current := list.head; current != nil; current = current.next {
currentData := current.data
status,err := compare(currentData,elem)
if err != nil {
return err
}
if status == Eq {
if pre == nil {
list.head = current.next
} else {
pre.next = current.next
}
deleted = true
} else {
pre = current
}
}
if deleted {
return nil
} else {
return OperationWithEmpty
}
}
链表的交点
寻找链表间的交点关键就是熟知链表相交的形状应该是Y字型,而不是X字型,链表若相交则会在第一个交点之后所以结点重合,故若两个链表相交的话,则至少尾指针指向同一个结点,由于两个链表长度可能不同,所以我们无法同时从头指针开始移动寻找交点,我们得先从长度较长得链表开始移动两个链表长度之差,然后两个链表同时移动,比较指针地址,若相同则找到公共结点,结束算法,若遍历结束还未找到,则不存在公共结点 若两个链表长度分别为 \(len1, len2\) ,则其时间复杂度为 \(O(len1 + len2) 或 O(max(len1,len2))\) ,空间复杂度为 \(O(1)\)func FindCommonNode(left LinkList,right LinkList) (n Node,err error) {
if left.IsEmpty() || right.IsEmpty() {
return nil,OperationWithEmpty
}
leftLength := left.Length()
rightLength := right.Length()
handle := func(short Node,long Node,diff int64) (node Node,err error) {
for k := int64(0); k < diff; k++ {
long = long.next
}
for {
if short == long {
return short,nil
}
short = short.next
long = long.next
if short == nil {
return nil,OperationWithEmpty
}
}
}
if leftLength <= rightLength {
return handle(left.head,right.head,rightLength - leftLength)
} else {
return handle(right.head,left.head,leftLength - rightLength)
}
}
链表的逆置
链表的逆置一般有两种做法,第一种是先建立新的头指针,然后在遍历过程中,将遍历的结点使用头插法插入到新建立的头指针,这样待遍历结束后,修改链表的头指针指向新遍历的头指针就完成了逆置操作,下面来看下代码:func (list LinkList) Reverse() (err error) {
if list.IsEmpty() {
return OperationWithEmpty
}
var newHead Node = list.head
head := list.head.next
newHead.next = nil
for ; head != nil; {
next := head.next
temp := newHead
newHead = head
newHead.next = temp
head = next
}
list.head = newHead
return err
}
func (list LinkList) ReverseBySwap() (err error) {
if list.IsEmpty() {
return OperationWithEmpty
}
pre := list.head
current := pre.next
pre.next = nil
for ; current != nil; {
next := current.next
current.next = pre
pre = current
current = next
}
list.head = pre
return nil
}
func (list LinkList) ReverseN(n int) (err error) {
if n <= 0 {
return OutOfRangeIndex
}
if list.IsEmpty() {
return OperationWithEmpty
}
var newListEnd Node = nil
var preNode Node = nil
currentNode := list.head
group := list.Length() / int64(n)
for k := int64(0); k < group; k++ {
newEndNode := currentNode
for i := 0; i < n; i++ {
nextCurrent := currentNode.next
currentNode.next = preNode
preNode = currentNode
currentNode = nextCurrent
}
if newListEnd == nil {
list.head = preNode
newListEnd = newEndNode
} else {
newListEnd.next = preNode
newListEnd = newEndNode
}
preNode = nil
}
//link the rest nodes
newListEnd.next = currentNode
return nil
}
链表的环
链表的环指的是在链表的尾指针指向链表的某个结点,导致链表出现环状,循环链表就是一个典型的带环的链表,链表带环一般像一个横放着的字母"P",对于链表环的问题主要讨论一个链表是否带环,环的入口点在哪,环的长度,下面按下方图片所示进行讨论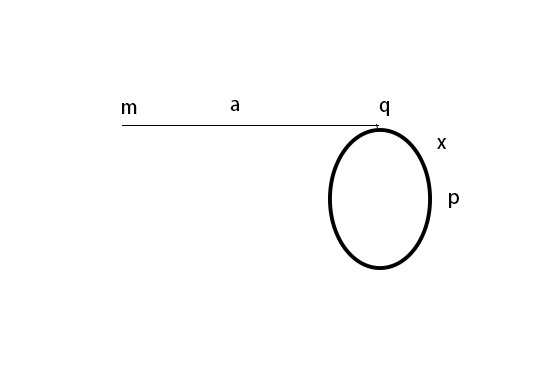
$$ 2s = s \ + \ n \ * \ r \quad (n是正整数) $$
通过图片符号所示我们知道
$$s = a \ + \ x$$
综上我们有
$$a = n \ * \ r - x$$
故在快慢指针在第一次相遇后,将慢指针从链表头部
\(m\)
点,以步调为1前进,快指针从相遇点以步调为1前进(此时快慢指针也可以用副本,毕竟它们已经脱离了实际含义,可以不再称谓其为快慢指针了),再次相遇点就为环的入口点,我们也可以同时求得
\(a\)
的值,而求环的长度也很简单,只需要在相遇点继续前进,记录再次回到相遇点的步数即为环的长度
注:判环算法也可以用于判断两个链表是否相交,将其中一个链表尾指针与另一个链表头结点相连,再判断是否产生了有环链表,若有环,则证明两链表相交
func (list LinkList) IsCycle() (bool) {
fast := list.head
slow := list.head
for {
if fast == nil || fast.next == nil {
return false
}
fast = fast.next.next
slow = slow.next
if slow == fast {
return true
}
}
}
func (list LinkList) FindLoopNode() (Node,error) {
fast := list.head
slow := list.head
for {
if fast == nil || fast.next == nil {
return nil,OperationWithEmpty
}
fast = fast.next.next
slow = slow.next
if fast == slow {
for slow = list.head; slow != fast; {
slow = slow.next
fast = fast.next
}
return slow,nil
}
}
}
func (list LinkList) LoopStartIndex() (int,error) {
fast := list.head
slow := list.head
for {
if fast == nil || fast.next == nil {
return 0,OperationWithEmpty
}
fast = fast.next.next
slow = slow.next
if fast == slow {
i := 0
for slow = list.head; slow != fast; {
slow = slow.next
fast = fast.next
i++
}
return i,nil
}
}
}
func (list LinkList) LoopLength() (int,error) {
fast := list.head
slow := list.head
for {
if fast == nil || fast.next == nil {
return 0,OperationWithEmpty
}
fast = fast.next.next
slow = slow.next
if fast == slow {
i := 1
slow = fast.next
for ; slow != fast; i++ {
slow = slow.next
}
return i,nil
}
}
}
总结
顺序表的算法主要是灵活运用索引的数学关键,链表的算法主要是灵活运用快慢指针及链表的结构
(ps:遇到优秀的算法和思路会在这和源码里补上)
(ps:遇到优秀的算法和思路会在这和源码里补上)
Next Post